One of the most requested topics for our Safe Withdrawal Rate Series (see here to start at Part 1 of our series) has been how to optimally model a dynamic stock/bond allocation in retirement. Of course, as a mostly passive investor, I prefer to not get too much into actively and tactically timing the equity share. But strategically and deterministically shifting between stocks and bonds along a “glidepath” in retirement might be something to consider!
This topic also ties very nicely into the discussion I had with Jonathan and Brad in the ChooseFI podcast episode on Sequence of Return Risk. In the podcast, I hinted at some of my ongoing research on designing glidepaths that could potentially alleviate, albeit not eliminate, Sequence Risk. I also hinted at the benefits of glidepaths in Part 13 (a simple glidepath captures all the benefits of the much more cumbersome “Prime Harvesting” method) and Part 16 (a glidepath seems like a good and robust way of dealing with a Jack Bogle 4% equity return scenario for the next 10 years).
The idea behind a glidepath is that if we start with a relatively low equity weight and then move up the equity allocation over time we effectively take our withdrawals mostly out of the bond portion of the portfolio during the first few years. If the equity market were to go down during this time, we’d avoid selling our equities at rock bottom prices. That should help with Sequence of Return Risk!
So, will a glidepath eliminate or at least alleviate Sequence Risk? How much exactly can we benefit from this glidepath approach? For that, we’d have to run some simulations…
Background on glidepaths
Target date funds use a time-varying asset allocation depending on the participant’s age. The idea is that young investors can and should take on more risk and hold a higher portfolio share in equities. Then, as retirement approaches, investors shift more into bonds to reduce risk. In fact, you don’t even have to do this shift yourself; Vanguard or whoever your provider may be will do it for you! Here’s Vanguard’s take on the glidepath, see chart below. The equity share (domestic plus international) in their target date funds starts at around 90%, drops to around 50% at the traditional retirement age of 65 and then further drops to 30% by age 72.
But recent research has shown that Vanguard (and many other providers of target date funds) actually got it wrong, at least for the post-retirement glidepath. The glidepath of equity weights should ideally start to increase (!) again once you retire. Michael Kitces wrote about this topic (on his blog here and here and in an SSRN working paper joint with Wade Pfau) and proposed to keep the minimum equity share at or around the retirement date before starting to raise the equity weight again during retirement.
The rationale is that the rising equity glidepath in retirement would be insurance against sequence of return risk. After all, the number one reason retirees run out of money is bad returns during the first few years of retirement. A low equity allocation shields you from short-term equity volatility, but longer-term you will need the high equity share to make it through 40, 50 or even 60 years of retirement. So, a dynamic stock/bond share would thread the needle to achieve both long-term sustainability and short-term protection.
Of course, as with all of the traditional retirement research, it has limited use for the early retirement community. My experience has been that a lot of the research targeted at the traditional retirement crowd, calibrated to capital depletion over a 30-year horizon, is less applicable to the FIRE crowd. For example, Safe Withdrawal Rates have to be lower over a 60-year horizon than over a 30-year horizon. And, equally important, equity weights have to be higher over a 60-year horizon to ensure long-term sustainability. Case in point, the 30% equity weight at the retirement start and 60% in the long-term as indicated in the Kitces chart above would be way too low for early retirees!
So, when unhappy with the whole Kit(ces) and Caboodle of hand-me-down research, what am I supposed to do? If you want something done and done right, you just have to do it yourself! That’s where the Big ERN simulation engine comes in handy!
Simulation assumptions:
- Monthly data from January 1871 to July 2017.
- A 60-year retirement horizon.
- Retirement dates from January 1871 to December 2015 (with extrapolations using conservative return forecasts for bonds and stocks beyond July 2017).
- Final value targets of 0% (Capital Depletion), 50% of the initial real value and 100% of the initial portfolio (in real terms).
For each of the 1,700+ cohorts, we calculate the safe withdrawal rate, i.e., the initial withdrawal percentage that exactly achieves the final target value after 60 years, assuming withdrawal amounts are adjusted for CPI-inflation regardless of the portfolio performance. As usual, we calculate the SWRs for the 21 different static Stock/Bond allocations (0% to 100% stocks in 5% increments). But we also simulate a total of 24 different glidepaths, comprised of the different combinations of glidepath parameters:
- Two different end points: 80% and 100%. Why not lower end points? As we will see later, the long 60-year retirement horizon necessitates a much higher (long-term) equity weight than the often-quoted 60% or even 50%.
- Three different starting points: 20, 40 and 60 percentage points below the end point.
- Two different slopes. Notice that I had to increase the slopes for the glidepaths that cover more ground, otherwise, the transition would take way too long:
- 0.2% and 0.3% per month for the glide paths starting 20 percentage points below the max,
- 0.3% and 0.4% for the paths starting 40 percentage points below the final target,
- 0.4% and 0.5% per month for the paths that start 60 percentage points below the final target.
- Two different assumptions for the glidepaths: Passive vs. Active
- Passive means that we stubbornly increase the equity weight every month by the slope parameter.
- Active means that we increase the equity share only when equities are “underwater,” i.e. when the S&P500 index is below its all-time high. We want to avoid shifting out of bonds too early, i.e., before the market peak and then having insufficient bond holdings when equities take a dive.
The “active” glidepaths, of course, are dependent on the retirement cohort. The transition from, say 60% to 100% equities would take a little bit longer depending on how equities perform during that time, see a sample of active glidepaths for the January 1965 to January 1980 cohorts below:
Results:
Let’s start with the failure rates of our preferred safe withdrawal rate, 3.50%. In the chart below, I plot the failure rates of three static equity weights, 60%, 80%, 100%, as well as the various glidepaths. Those with a final equity weight of 80% at the top and with a final equity weight of 100% at the bottom. First, let’s do this for all 1,700+ monthly retirement cohorts regardless of equity valuations (“All CAPE”):
Some patterns emerge from this chart:
- There will be at least a few glidepaths with lower failure rates than the static allocations. It seems that the 80% to 100% and 60% to 100% glidepaths deliver consistently lowest failure rates, regardless of the final value target!
- Who would have thought that the maximum long-term equity weight delivers the lowest risk? This goes back to the superior equity long-term expected returns; once you make it through the shaky first 5-10 years exposed to sequence risk you want to max out the equity weight!
- The very long transitions over 60 percentage points (20 to 80% and 40 to 100%) tend to be pretty consistently inferior to the other glidepaths. The 20 to 80% glidepaths are even inferior to the static 80% and 100% allocations! Apparently, the initial stock weight was too low and/or the transition took way too long (even with the accelerated slopes of 0.4% and 0.5%!)
Do glidepaths become more useful when the Shiller CAPE is high?
As we have pointed out numerous times before (for example, in Part 3 of the series), the Shiller CAPE is strongly correlated with safe withdrawal rates. Plain and simple: Sequence of Return Risk is elevated when the CAPE ratio is high! Is that also reflected in the glidepath performance? You bet, see chart below:
- First, notice that the failure probabilities of the static rules are now much higher due to the higher CAPE ratio. Even a capital depletion target fails with about 17%, 7% and 12% probabilities for the static equity weights of 60%, 80%, and 100%, respectively.
- Most glidepaths pretty consistently beat the static equity weights. The consistently best performers are the 60 to 100% glidepaths and the active glidepaths perform slightly better than the passive ones. The failure rates are less than half those in the static allocation simulations!
- The 20 to 80% and 40 to 100% glidepaths are still inferior to the other glidepaths. And the 20 to 80% glidepaths are inferior to the even the static asset allocations.
More on the distribution of SWRs: Failsafe and other SWR percentiles
A lot of very risk-averse retirees like to set their SWR to the failsafe SWR in historical simulations. That seems very conservative, but I can see where they are coming from. If your strategy would have handled the Great Depression, the nasty 1970s/early 1980s, and the volatile 2000s you can probably also use it in 2017 without too much worry!
In the table below, I calculate the failsafe SWR, i.e., the minimum historical safe withdrawal rate (60-year horizon, 0% final value), as well as some other percentages (1st percentile, 5th, 10th and 25th). So, for example for the 80% fixed equity allocation, the absolute lowest historical SWR would have been 3.14%. A 3.43% initial SWR would have failed 1% of the time, 3.59% would have failed 5% of the time, 3.86% would have failed 10% of the time and 4.48% would have failed 25% of the time. I don’t think planning for a 25% or even 10% failure probability is very prudent – personally, I try to target a failure probability in the single digits, e.g., 5% – but I display the numbers just in case someone wonders.
The left portion of the table is for all possible retirement start dates (about 1,700 of them, monthly data from 1871 to 2015). The right part of the table is for those months when the Shiller CAPE ratio is above 20. In the top portion of the table, I also marked with green boxes the maximum value among the static asset allocation rules in each column. Notice how the maximum in each column is at between 75 and 100%! To make it through a 60-year retirement, you can’t have a 60% or even 50% equity share. That only works for 30-year horizons! Also notice that with a CAPE>20 all numbers in the far right column are <4%, so the 4% had a failure rate of over 25% regardless of the equity glidepath!
In any case, 60 to 100% glidepaths generate the consistently best SWRs. For the über-conservative FIRE planners who are looking for the failsafe 60-year SWR conditional on our current 20+ CAPE environment, a fixed 75% stock allocation would allow a withdrawal rate of only 3.25% and that’s already the max over the static allocation paths! The 60 to 100% glidepaths would have allowed between 3.42 and 3.47%. That’s an improvement of between 0.17% and 0.22%. It doesn’t sound like much but it’s an improvement of between 5 and 7% of annual withdrawals. Not bad for doing a simple glidepath allocation.
Likewise, if I’m OK with a 5% failure probability conditional on a CAPE>20, then the static stock allocation of 80% would give me an SWR of 3.47%. The glidepaths would have allowed between 3.57% and 3.63%. Only an additional 0.16%, but that’s about 5% more consumption every year!
So, we won’t get all the way to 4%, but we bridge about one-third of the way, simply by playing with the asset allocation over time.
A small caveat, though; the calculations raise the question: do we get something for free? Is this some sort of a money-making arbitrage machine? Of course not! A glidepath will deliver a higher safe withdrawal rate if you have an equity drawdown early on in retirement. But the opposite is true as well. That 60 to 100% glidepath that performed so well during the major Sequence of Return Risk disasters will also underperform if stocks rally during the first few years of retirement. Let’s look at the table below that displays the SWRs of the 60%, 80% and 100% static equity weight and the 60 to 100% glidepath with a 0.4% monthly slope conditional on equity performance. As we already know, it beats the static equity allocation rules significantly when retiring at the market peaks (=worst time to retire). But the glidepath also falls significantly behind the 100% equity allocation if you were to retire at one of the three market bottoms (=best time to retire). It handily beats the constant 60% allocation and is slightly inferior to the 80% constant equity allocation. But I wouldn’t really care too much about falling behind in that case. You still get phenomenal SWR, just a little bit worse than the even more phenomenal SWRs of the 100% equity allocation.
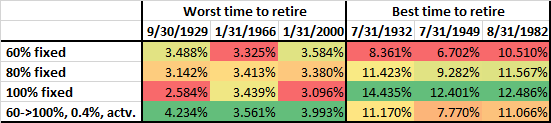
Conclusion
Early retirees need the power of equity expected returns to make the nest egg last for many decades. Even more so than the traditional retiree at age 65! But that exposes us to Sequence of Return Risk. An equity glidepath can alleviate some of the negative effects of Sequence of Return Risk. But it shouldn’t come as a surprise that you will never completely eliminate the risk. For a given withdrawal rate, say 3.5%, we can only reduce the failure rate while leaving some residual risk. And likewise, the 4% rule would still not be safe for today’s early retirees even with an equity glidepath.
Moreover, an equity glidepath is like an insurance policy. A hedge against a tail event! On average it will cost you money, but if and when you need it the most it will likely pay off. Exactly when the static stock/bond allocation paths had their worst sustainable safe withdrawal rates you get slightly better results but you also give up some of the upside if the equity market “decides” to rally some more right after your retirement. But that’s a good problem to have!
It appears they used 85% equities which explains some of the differences, though its not very clear on why they deemed this to be the “optimal” rate.
Its pretty cool to see an old school early retirement site, it seems to have held up pretty well more than two decades later through 3 recessions.
With “they” you mean Kitces and Pfau? It looked like they do the GP with a smaller than 85% equity share.
Hello big ERN!
I’m a constant reader of your blog, and it helps me a lot!.
I got a few questions as I’m about to start my early retirement in a few years:
1. I’m a non-US citizen and since I buy my stock ETFS in USD, I would like to know, do currency exchange rates impact the SWR?.
My country’s currency has been strengthening against the dollar for the past 20 years.
On the other hand, the inflation in my country has been lower than in the US.
If the above stays that way, what does it mean for my SWR?.
2. The asset I use for bonds is an asset which only maintains the real value of the money (with no any additional real return, it gives you exactly the CPI for my country).
Would it work well for let’s say 60%->100% GP?.
Since it would never give you any additional real return above the CPI, can it jeopardize the success of my portfolio? should I use a riskier asset in my bonds segment because of that concern?
3. Currently I have around 75% stocks.
I buy only stocks with my income, and my bond allocation is fixed to a certain amount of money without contributions and rebalances, therefore increasing my stocks % (because I don’t have a set date for retirement).
So, if upon retirement, I would be lucky and have 80-90% stocks and reach a low SWR, say, the fail-safe or 1% risk of failure, is it ok to just stick with this stock allocation as a fixed allocation, or is it still better to do a glidepath to 100%?.
4. Since all the researches has been done on the US stock market, would investing in all world stock Indices like ACWI make a notable difference in the SWR?
thank you very much for your helpful blog!
I don’t have any specific recommendations for people living outside the US. The simulation is based on US returns. I lack the non-US equity returns, the FX rate between US returns and your specific country’s currency.
If someone has indeed a bond option to invest in a 0% real returns, month-after-month, you can use the “custom” series column and set the columns equal to 0% (column R or S in the tab “Stock/Bond Returns”).
4: I added the non-US returns post 1970 in my Google Sheet
Thanks for your reply.
You’ve misunderstood me regarding my 1st question.
I didn’t mean that I invest in non-US equity, I invest all of my equity portion in an ETF that tracks all world index, and I buy it in USD (I convert money from my currency to USD).
When I’d withdraw money for living, I’d convert the USD received from the units sold to my currency again, hence I was wondering how and if the FX rates affects the SWR (in the last 20 years, the USD has weakened by 25% against my country’s currency). Is that something to be concerned about regarding SWR?.
If so, can inflation rate differences also contribute to the SWR differences? (our inflation has been lower than in the US for the last 20 years 35% here vs 58% in the US).
I’d be very glad if you could reply to my 3rd question as well.
thank you again for your help!.
Currently, the world index would be roughly modeled through 50% US equity plus 50% non-US, so just use that split in the Google Sheet.
I have neither FX rates nor CPI for any country, much less for all countries that people might be interested in.
If someone wants to “hack” my Google Sheet and incorporate their own country CPI and the FX rate between the USD and their own currency (good luck finding 100+ years of data!), they can certainly incorporate that into their own sheet. I am currently not planning to provide that feature.
Alternatively, you could assume long-term purchasing power parity and pretend that any differences in inflation will eventually be reflected in exchange rates. Then you can indeed use the USD-based and US-CPI-based calculations.
As far as the glidepath is concerned, if you start with 80-90% equities at retirement, you don’t really have much of a GP. Will not make much of a difference.
Thanks again,
Regarding your alternative suggestion (assuming long-term purchasing power parity and pretend that any differences in inflation will eventually be reflected in exchange rates),
Do you suggest this assumption because I don’t have much of a choice, or because it has a basis in reality?.
Not much of a choice. That’s a good way of putting it. The only way out would be for UK investors who indeed should have access to long-term time series for both GBPUSD exchange rates and GBP-based inflation measures.
Detail question: what is the Non-US equity series used in the spreadsheet? Developed ex-US?
MSCI World ex USA. And that’s Developed markets only.
Hi Big ERN,
Have you come across Michael Edleson’s Value averaging strategy? I am really inspired by your rising glidepath approach. But after I learnt about your approach I stumbled upon the value averaging concept and I found striking similarities! Only different is while you are targeting a equity ratio path, Value averaging strategy targets a dollar amount path.
So what I did is 1st I used your rising equity glidepath and plotted the expected equity ratio path and then I used the value averaging strategy to get the exact dollar amount path.
So I kind of married the 2 strategies. Your strategy is amazing for its simplicity. But I find using the value averaging strategy in combination of yours allows you to invest more amounts in a bear market.
For example: lets say you are 50:50 and next month you need to hit 51:49 also the amounts are currently you have 500k:500k and you need to hit 510k:490k with your glide path approach, in case markets were static. In value averaging approach also you need to 510k:490k if markets were static.
Now imagine a 20% correction.
With the glide path approach:
Before rebalancing your equity:bond after a 20% correction becomes: 400k:500k and after rebalancing to 51:49 it becomes 459k:441k
With the value averaging approach, you are supposed to hit 510k!
So your allocation becomes 510k: 390k.
So while your strategy appears very similar to value averaging, during normal markets, but in case of crash, the value averaging strategy ends up deploying a lot more money into the markets.
I am actually implementing this strategy right now, while I am working and have inflows coming in. So I find the value averaging superior to glide path approach. Would like to know your thoughts, if you have considered this.
Thanks in advance!
Heard about value averaging. Slightly false advertizing. Though I like the “value” tilt of putting in more money when the market is down. But it’s only useful if you actually HAVE the money. Not workable for most ordinary folks like the average 401k saver.
But I agree that the flavor is somewhat similar if you do the VA only on the equity portion (not the overall portfolio, because that would mean you have to contribute instead of withdraw if there’s a bear market in retirement).
So, the flows from bonds into stocks after a stock market drop indeed look and feel a bit like VA. But keep in mind that you might get B->S flows even with a static allocation if the stock market drop is fast anddeep enough. Think 2007/8/9 or Spring 2020. It’s simply a rebalancing from expensive bonds to cheap stocks you’ll get with both a static and rising equity target allocation.
Hi Big ERN,
I’m curious if you think the lower current real yield of bonds would reduce the effectiveness of a 60%-100% glidepath? I intend to retire at the end of the year, and I think I’m going to go with a 3.1% SWR combined with the 60-100 glidepath. I feel that it’s fairly conservative, but I don’t want to have any financial anxiety if the stock market tanks right after I retire. I’ll probably bump the withdrawal rate up if the first few years of returns are good.
Yes, good point. But: The bond allocation was never meant to boost returns. Whether you make +1% real or -1% real, it’s not going to make a huge difference. It’s the diversification part, i.e., bonds gani when stocks lose, that will do the job.
Dear Big ERN,
Thank you for this awesome SWR series, that’s a real goldmine for FIRE adepts 🙂
I’ve got a question for the GP – the increasing percentage of allocation is supposingly done by shifting from bonds to equity, i.e. selling bonds and buying stocks. That works if the market is static. But then, if equity market rises, and your allocation changes to the desired proportions by itself, do you simply do nothing? Or if it changes above your target equity allocation, do you then do a standard rebalancing by selling stocks and buying bonds to achieve your new, updated (increased monthly) target allocation? Am I getting this right, that you simply change your target allocations monthly and rebalance accordingly?
Also, I don’t know if you’ve put any thought to it, but in the real world transaction fees might actually increase the cost of such an approach (the monthly rebalancing along the GP) – did you consider a GP with quaterly steps? Would it make much difference? (I don’t suppose so since it’s been shown in various sources that more frequent rebalancing doesn’t necessarily provide better outcomes, if not worsen them)
Thanks for all your work and keep it up!
Thanks.
This post “How often should we rebalance our portfolio? – SWR Series Part 39” will answer many of your questions:
https://earlyretirementnow.com/2020/08/05/rebalance-swr-series-part-39/
I’ve been stuck on an apparent paradox contained in this glidepath strategy – that two retirees, with identical financial situations, at a given point in time, have different optimal asset allocations. I may have at least partially worked it out just now, though I’m interested in any arguments that fully resolve this puzzle, or refute what I’ve put forward so far.
Imagine two investors, X and Y, in 2030. Both are 40 years old. Both are planning for a 90 year life expectancy.
X retired in 2021, at age 31, with a WR of 3.5%. Following this research, X took a 60->100, 0.4% passive, glidepath approach. Now at age 40, X will be in 100% equities for the rest of X’s life, just as the research suggests. Both stocks and bonds have had 0 real returns for the last 9 years, and so X is still at a 3.5% WR.
Y is retiring right now, in 2030, with a WR of 3.5%. Following this same research, Y will also take a 60->100, 0.4% passive, glidepath approach, and so Y has shifted to 60% equities.
The apparent paradox is that these two investors, each with a 3.5% WR and a 50 year remaining investment horizon in 2030, should have different asset allocations. But in 2030, there is seemingly nothing financially distinct about them!
My partial reconciliation is that when A retired, A had no way of knowing that real returns would be flat for the next 9 years. And so while things look weird in 2030, in 2021, the potential distribution of 9-year outcomes still logically supported the X’s glidepath. Likewise, as Y retires (in 2030), the same is true for Y’s glidepath.
And yet there’s still something fishy going on in this hypothetical 2030. It seems like Y is about to spend 9 years benefitting from reduced SORR, while X is about to confront the full, unmitigated force of it. Why?
Should we extend this research to examine “resetting glidepaths”, which return to 60% under some set of flat/falling market scenarios? Intuitively, that seems problematic, since it leaves people who have been victim to early retirement drops with less of a chance to get back to the high equity levels they need for long-term success. But at least it would give us a chance at resolving the puzzle above.
(I acknowledge that this post studies 60 year horizons, and X and Y aren’t quite that, but I expect they’re close enough that the ideal glidepath doesn’t change much for either of them).
Point well taken. It’s the problem that a lot of basic glidepath strategies face: They violate Bellman’s Principle of Optimality (see https://earlyretirementnow.com/2020/11/09/what-is-wrong-with-target-date-funds/).
The solution would be to do a more time-consistent, dynamic optimization. That’s actually one project I’m working on in my little consulting side gig for a FinTech startup. 🙂
Yes, Bellman’s Principle – exactly that! I had only ever seen it in the context of trajectory optimization in robotics, but I see that it works here, too. Neat. Thanks for the confirmation.
Amazing how generally applicable that Bellman/dynamic programming stuff is! 🙂
Very happy to hear that you’re doing research on dynamic allocation. Hopefully, you will publish the results of that work here as well (sorry if you have already, I’m working my way through the series). Your CAPE based withdrawal research showed the power of dynamic/fundamentals based approaches on the withdrawal side and you made the comment earlier that you ultimately want to move to the NE side of your diagram of static and dynamic approaches. Given the prediction powers of CAPE and the importance you put on it for determining a safe withdrawal rate, it seems silly to pre-program in an equities glidepath rather that using an equation that uses CAPE like your CAPE-based withdrawal equation A + B * CAEY.
Hi big ERN
Really clear post and I now understand the mechanics of glidepaths and how to move from 60%->100% in retirement.
My question is about pre-retirement:
As me and Lazy FI Mum both work, we can handle lots of volatility so in the accumulation stage we have 100% in stocks, how do you suggest moving towards 60% as we get closer to retirement? A reverse glidepath?
Correct. That’s what I write about in Part 43:
https://earlyretirementnow.com/2021/03/02/pre-retirement-glidepaths-swr-series-part-43/
Thank you for the detailed analysis on Glidepaths – which specific bond / bond funds are you using to backtest in these examples? Is it something similar to a total bond market fund like FTBFX? Have you considered what failure rates would look like if we used a risk parity type approach similar to Hedgefundie’s adventure?
I use the 10-year Treausry benchmark bond. Gov bond only, no corporates. IEF would be a good approximation.
That;s way too much equity allocation for my taste but nice work anyway
Well, with too much bonds, you don’t want leverage. You just sell the bonds. 😉
Agreed but I think I like Kitces approach better. He always say, you want to plan for safety or you want to plan for wealthy. I’m definitely don’t mind sacrificing a few millions in the end for Safety and assurance I won’t run out of money and if that means getting as low as 30% equity when I FIRE, that’s ok with me..I’ll slowly glad back up to 65% equity after 10yrs into FI
besides with CAPE Shiller PE currently at almost 40, the second highest in history, being over exposed to equity might be a too high of a price to pay if shit hits the fan in your 10 first years.
Bond yields are also low! 🙂
Due respect, Kitces got the concept correct here, but the numbers wrong. A big portion of this is that he uses Monte Carlo sims rather than historical data, as ERN points out well.
A second portion – which Kitces himself *partially* realizes in a another post – is that in his mind hit’s not an option to “ever” get the equities allocation higher than a traditional retiree “traditionally” would. and so this means he sets the initial equity weights too low, since he’s going to top out at 60% or 70%.
But IMO the other reason – that ERN gets but often doesn’t explain [and imo never explains well! 🙂 ] is that regardless of whether it’s an early retiree or a regular retiree, that 100% equity weighting is *only* for those times when the market is down 35%+.
Otherwise when the market isn’t down big, THERE IS NO SENSE IN THE WORLD THAT 100% EQUITIES IS SAFER. (And ERN has other posts – like Part 38 – when he says basically that.) It was clearly just easier / more practical for him to run the simulation that way!
The simulation and explication are accurate, it’s just that most people interpret it incorrectly. Yes, if the market has soared and your current effective withdrawal percentage has dropped fro 3.4% to 2.7%, it might be safe enough to keep your portfolio at 100% equities, but unless your goal in that case is to leave a larger legacy bequest, it’s not actually *safer* to keep 100% in equities.
In reality, if your portfolio is up to a new inflation-adjusted high, to be safer you should reset to the initial glidepath weights – and in fact can now safely withdraw more (in dollars) than before!.
And if the market is down somewhat but isn’t down big 5 or 7 years into the glidepath time, it will certainly be safer to pause your equity weight at, say, 70% or 75% or 80% rather than have it continue to 100%. For that matter, if the market does crash 40%+ and you do get your equity allocation to 100%, if and when say 2 years further on it has recovered substantially, it will at some point be safer to glidepath from 100% *down* to 80% or 70% equities. But again, this is too hard to put into a simulation.
…and not all that easy to explain in what are already fairly long blog posts.
In any case, at 30% starting equity weight, you are in fact taking more risk, not less, unless of course you are confident in your market timing or in your belief that the future will be worse than anything that’s occurred in the past.
Yes, good point. Maybe I should write a post on that:: Under what conditions would 100% equities be better 75/25?
That would be great!
An update to the glidepaths post(s) that incorporates your more recent thoughts on increasing consumption would be even better. “Flexibility” vs. monotonically increasing consumption vs.”ratcheting, e.g.
A way to tie the glidepaths stuff more directly into an updated Part 28 Google sheet would be best of all! 🙂
OK, good suggestions! 🙂
Hi Karsten,
First off, thank you for the great post!
Reading through it, I was thinking that the glidepath approach is very similar to just living off the bond portion of your portfolio for a given time (5-11 years) at the beginning of your retirement and let the dividends of the stock portion reinvest automatically during that time (assuming a dividend yield of 1.4 – 2.8%). Is that an accurate statement/comparison or am I totally off base?
The two look very similar, for sure. So, the GP is not very different from a bucket strategy where you liquidate the safe buckets.
Hi ERN!
Can’t thank you enough for the work you do!
For the active glidepath, is there a threshold for considering equities to be “underwater?” I ask because even during a raging bull market, short term fluctuations will often leave equities beneath the all time high. Is it judged by a certain percentage drop from the all time high? Thanks!
Underwater means under the all-time-high. You can get really fancy with more complicated rules but i wanted to keep it simple.
Thanks for the post! The 60/100 glidepath looks very compelling, but I’m also considering a non-linear variation. I propose starting at 40% bonds and adjusting according to the formula:
(New bond %) = (Bond % from last year) x (Constant factor)
We could experiment with different constant factors. I’m thinking of 0.85 as a starting point, since this would give results somewhat similar to the linear 60/100 glidepaths in this post: 60%, 66%, 71%, 75%, 79%, 82%, 85%… .
This non-linear glidepath has some nice properties. The slope of the glidepath is proportional to the sequence risk. In other words, the slope is greatest early in retirement when the sequence risk is greatest, then gradually decreases as the sequence risk decreases. Later in retirement, the equity percentage would asymptotically approach 100%, but never quite reach 100%. Thus, the glidepath would continue to provide some benefit. This benefit would gradually erode, but it least it has no abrupt endpoint.
Have you considered this kind of non-linear glidepath? Does my intuition sound correct or are there other considerations that I overlooked?
Haven’t considered this yet. Sounds premising. Because, as you say, the effect of the GP dies down just as the sequence Risk. Will think about how to implement that in the code.
What type and maturity of bonds do you use for your Bond returns?
10y benchmark Treasury Bonds, total returns.
Have you looked at how starting retirement with a glidepath when term treasury rates are low affects the SWR compared to when rates are higher?
Is there a point when treasury rates are so low that 100% stocks becomes to best allocation (especially for long retirements? If so, what is that cutoff?
Good question. Haven’t looked at that yet. You may be right, though in that when yields are low, there is relatively little risk of an impending meltdown. The meltdown is likely behind us, hence the low yields.
But of course, the 10y yield has now almost normalized again, so not really relevant for us n the current environment.
Do you have a copy of the Sheet you do the Glidepath calculations with? I wanted to see how it changes for different bequest sizes at the end.
You can simulate a single gp cohort in the Google Sheet. But the computiations here are done with Matlab, not a single sheet.
Thanks a lot for this great simulation ERN!
I am wondering how you implement the GP in these calculations? This could be done through rebalancing after each month and then withdraw from that or use the withdrawal itself to help the rebalancing. There is probably not much difference but avoiding the rebalancing could lower the fees.
The order (rebalance first and then withdraw vs. withdraw first and then rebalance) doesn’t matter. They both give you the same result.
Another issue: how about you only withdraw (from the part of the portfolio with higher than planned weight) and do no rebalance after that or rebalance only infrequently. That’s not what I do here in my calculations in Parts 19/20. But one can show that this kind of rebalance rule doesn’t make a lot of difference either. See Part 39 of the series.
Thanks a lot for your quick answer! I will check part 39!
Thanks for your quick reply. I will check out part 39 for more details!
Is there any particular reason you chose 10 year bonds over longer or shorter duration bonds? Have you tested short, intermediate, and long term bonds to see if they have higher SWRs than using 10 year bonds?
Yes, I have tested 30Y bonds and shorter-duration. 10y seems to be best diversifier.